E = mc2 dünyanın en ünlü denklemi, peki gerçekten ne anlama geliyor? "Enerji eşittir kütle çarpı ışık hızının karesi." En temel anlamıyla bu denklem, enerji ve kütlenin (madde) birbirinin yerine geçebileceğini söyler. Bunlar aslında aynı şeyin farklı formlarıdır. Doğru koşullar altında enerji kütleye dönüşebilir ve bunun tersi de geçerlidir. Biz insanlar onları bu şekilde görmüyoruz. Örneğin bir ışık demeti ile bir elma nasıl aynı şeyin farklı biçimleri olabilir? Ancak doğa öyle görüyor.
E = mc²'nin Anlamı
Albert Einstein'ın denkleminde yalnızca üç harf ve bir sayı var:
- E = Enerji
- m = Kütle
- c2 = Işık hızının karesi (Latince "hız" demek olan celeritas terimidir. Işık hızı kendisiyle çarpılır)
Maddenin içindeki enerjiyi bilmek için neden kütlesini ışığın hızıyla çarpıyoruz? Bunun nedeni elma gibi bir madde parçasını saf enerjiye dönüştürdüğünüzde ortaya çıkan enerjinin ışık hızında hareket etmesidir. Saf enerji, ışık veya X-ışını gibi bir elektromanyetik ışınımdır ve bu elektromanyetik radyasyon 300.000 km/saniye sabit hızla hareket eder.
Öyleyse neden ışık hızının karesini alıyoruz? Enerjinin doğasıyla ilgilidir. Bir şey başka bir şeyden dört kat hızlı hareket ettiğinde, dört kat daha çok enerjiye değil, 16 kat daha çok enerjiye sahip demektir. Yani o rakamın karesine. Yani ışık hızının karesi, maddenin içindeki enerjinin dönüşüm faktörüdür. Işık hızının karesi çok büyük bir sayı olduğu için (90.000.000 km/sn2) en küçük kütleli maddenin enerjisi bile akıllara durgunluk vericidir.
Ortaya çıkan enerji çok büyüktür: Bir ataşın içindeki atomların her birini saf enerjiye dönüştürebilseydiniz (geride hiç kütle bırakmadan) ataş 18.000 ton TNT gücünde enerji verirdi. Bu enerji kabaca 1945'te Hiroşima'yı yok eden bombanın boyutu kadardır. Bununla birlikte Dünya'da bir ataşı veya başka bir nesneyi tamamen enerjiye dönüştürmenin pratik bir yolu yok. Bunun için Güneş'in merkezinden daha yüksek sıcaklık ve basınç gerekli.
E = mc2'nin Önemi

E = mc2'nin önemi ve etkileri derindir. Yüzyıllar boyunca bilim adamları enerji ve kütlenin tamamen farklı ve birbiriyle ilgisiz olduğunu düşündüler. Einstein ise aynı şeyin farklı biçimleri olduklarını göstererek evren anlayışımızı değiştirdi. Einstein'ın kendisi bile bu bulguya şaşırdı, denklemi "eğlenceli ve baştan çıkarıcı" olarak nitelendirdi ve "Tanrı buna gülüyor mu ve bana oyun mu oynadı" diye merak etti.
Radyoaktif bozunma, nükleer fisyon veya füzyon tepkimesi yaşandığında başlangıçtaki kütle son kütleden büyük olur. Yani kütlenin korunumu yasası geçersizdir. E = mc2'ye göre aradaki garip kütle farkı açığa çıkan enerjidir. Bu gerçek, bozunmakta olan bir uranyum fisyon bombasından, Güneş'teki nükleer füzyona ve madde-antimadde çarpışmasına dek her şey için geçerli. Bir denklemdeki yok olan kütle miktarı enerji olur.
E = mc2, enerjinin hiçlikten kütle yaratmak için kullanılabileceğini anlatıyor. Bir elektronu ve fotonu yeterince yüksek enerjiyle çarpıştırırsanız ortaya bir elektron, bir foton ve yeni bir madde-antimadde parçacık çifti çıkacaktır. Yani iki yeni dev parçacık oluşur:
- elektron, proton, nötron gibi bir madde parçacığı,
- ve pozitron, antiproton, antinötron gibi bir antimadde parçacığı,
Bu parçacıklar ancak yeterli enerjiyle ortaya çıkıyor. CERN'deki LHC gibi parçacık hızlandırıcıları Higgs bozonu veya üst kuark gibi kararsız ve yüksek enerjili yeni parçacıkları bu şekilde aradı: Saf enerjiden yeni parçacıklar yaparak.
Genel Göreliliği Bulmasını Sağladı
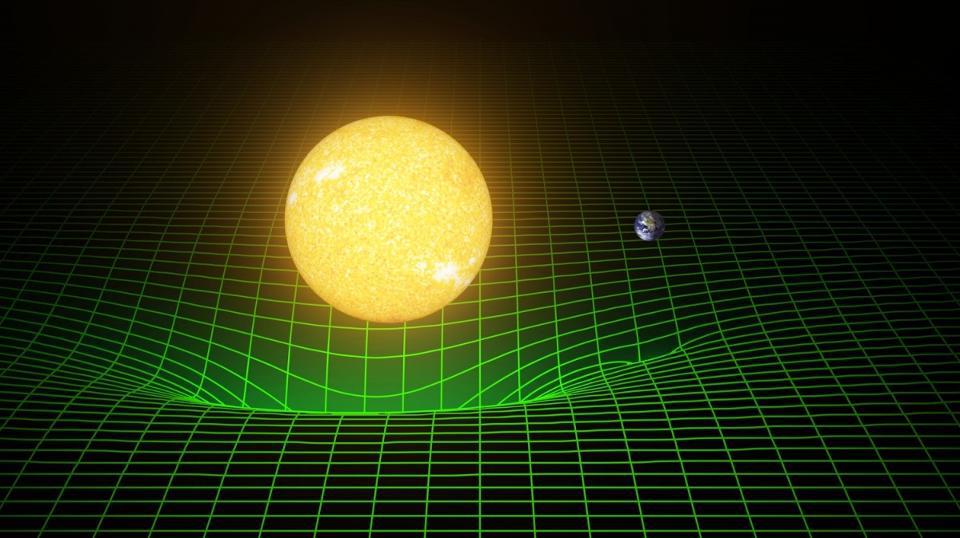
E = mc2'deki kütle-enerji denkliği aynı zamanda Einstein'ı en büyük başarısına götürdü: Genel Görelilik. Aynı kütledeki bir madde parçacığı ile bir antimadde parçacığını çarpıştırırsanız enerjisi E = mc2 ile bulunabilen fotonlar üretilir. Şimdi, bu parçacık/antiparçacık çiftinin uzayda düşüyormuş gibi hızla hareket ettiğini ve sonra Dünya yüzeyine yakın bir yerde çarpıştıklarını hayal edin. Bu fotonlar şimdi daha yüksek enerjiye sahiptir çünkü yalnızca E=mc2'den gelen E'den değil, aynı zamanda düşerek kazandıkları kinetik enerjiye sahipler.
Einstein, enerjinin korunumu ile yerçekimsel kızıla kaymayı keşfetti (ve maviye kayma): Einstein'a göre yerçekimi uzayı bükerek kuyu oluşturur ve yaklaşan enerjiyi sıkıştırarak şiddetini (yani rengini) değiştirir. Isaac Newton'ın yerçekimi yasası bunu açıklayamaz ancak Einstein'ın Genel Göreliliği'ne göre uzaydaki bir eğriliğe yani yerçekimi alanına düşmek o maddeye enerji kazandırıyor ve yerçekimi alanından çıkması enerji kaybettiriyor. Uzayda hareket eden nesnelerin enerjisini bulmak için E = mc2 denklemine momentum ve yerçekimini dahil ettiğinizde artık tüm evreni anlayabiliyorsunuz.
Einstein'ın enerji ve kütleyle ilgili ilk makalesinde, E = mc2 aslında hiçbir yerde görünmez. Einstein formülü m=L/c2 olarak yazmıştır. Çünkü Einstein, enerji için "E" yerine "L" (Lagrange için genel bir enerji biçimi) kullanıyordu. Daha sonra "L"yi "E" ile değiştirmiş, değişkenleri yeniden düzenlemiş ve denklemin ünlü formu ortaya çıkmıştır.
E = mc² Hakkında Sık Sorulanlar
E = mc² kısaca nedir?
E = mc², Almanya doğumlu fizikçi Albert Einstein'ın özel görelilik teorisinde kütle ve enerjinin aynı fiziksel varlık olduğunu ve birbirlerine dönüştürülebileceğini ifade eden denklem. Denklemde, bir cismin artan rölativistik kütlesi (m) çarpı ışık hızının karesi (c2), o cismin kinetik enerjisine (E) eşittir.
Hareketsiz bir cismin enerjisi kütlesiyle nasıl ilişkilidir?
Hareketsiz bir cismin enerjisi, kütlesinin ışık hızının karesiyle çarpımına veya E = mc²'ye eşittir.
Kütle-enerji ilişkisi kütlenin enerjiye dönüştürülebileceğini ve tersinin de mümkün olduğunu nasıl ima eder?
Kütle-enerji ilişkisi, dönüşüm sonucunda bir cisimden enerji salınırsa, cismin kalan kütlesinin azalacağını ima eder. Tersine, eğer bir cisme enerji eklenirse, cismin kütlesi artacaktır.
Ne tür reaksiyonlarda durgun enerji diğer enerji biçimlerine dönüşür?
Durgun enerji sıradan kimyasal reaksiyonlarda diğer enerji formlarına dönüştürülür, ancak nükleer reaksiyonlarda çok daha büyük dönüşümler meydana gelir.
Nükleer füzyon reaksiyonlarında kütle-enerji ilişkisinin önemi nedir?
Nükleer füzyon reaksiyonlarında, atom çekirdeklerinin kütlesinin küçük bir miktarı E = mc²ye göre enerjiye dönüştürülür. Bu, Güneş gibi yıldızlara güç veren süreçtir.
Einstein E = mc² denklemine nasıl ulaştı?
Einstein, enerji ve kütlenin eşdeğer ve birbirinin yerine kullanılabilir olduğunu gösteren özel görelilik ilkelerini uygulayarak E = mc² denklemine ulaştı.
E = mc²'deki ışık hızının fiziksel önemi nedir?
E = mc²'deki ışık hızı, enerjinin uzayda seyahat edebileceği maksimum hızı temsil eder ve bu nedenle belirli bir kütle miktarından elde edilebilecek enerji miktarı üzerinde temel bir sınırdır.
E = mc² nükleer reaksiyonlarla nasıl ilişkilidir?
E = mc² denkleme göre atom çekirdeklerinin kütlesinin küçük bir miktarının enerjiye dönüştürüldüğü nükleer reaksiyonlarda açığa çıkan enerjiyi açıklar. Bu süreç güneşe ve nükleer enerji santrallerine güç veren şeydir.
E = mc² bir kara delik oluşturmak için gereken enerjiyi hesaplamak için kullanılabilir mi?
Evet, E = mc² bir kara delik oluşturmak için gereken enerji miktarını hesaplamak için kullanılabilir, çünkü kütle-enerji eşdeğerlik ilkesi kütle ve enerjinin tüm formları için geçerlidir.
E = mc² deneysel olarak nasıl doğrulanmıştır?
E = mc², nükleer reaksiyonlardaki kütle-enerji dönüşümlerinin gözlemlenmesi ve atom altı parçacıkların kütle ve enerjilerinin ölçülmesi de dahil olmak üzere çeşitli deneylerle deneysel olarak doğrulanmıştır. Nükleer reaksiyonlarda açığa çıkan enerji de denklemin geçerliliğinin kanıtıdır.
E = mc² evrenin temel doğasına ilişkin anlayışımızı nasıl etkiledi?
E = mc², kütle ve enerjinin aynı şeyin iki yönü olduğunu öne sürdüğü için evrenin temel doğasına ilişkin anlayışımız üzerinde derin bir etkiye sahip olmuştur. Bu, kütle-enerji eşdeğerliği kavramını içeren yeni teori ve modellerin geliştirilmesine yol açmış ve madde ve enerjinin doğası hakkındaki düşüncelerimizi temelden değiştirmiştir.
E = mc² karanlık enerji olgusunu açıklamak için kullanılabilir mi?
E = mc² karanlık enerji olgusunu açıklamak için kullanılabilir, çünkü boş uzayın kütleye eşdeğer enerji içerdiğini öne sürer. Bu enerji, karanlık enerjinin önemli bir yönü olan evrenin genişlemesinin hızlanmasına katkıda bulunabilir.
Kaynaklar: