Fraktal Nedir? Özelliği, Önemi ve Doğadaki Örnekleri

Fraktallar yalnızca doğa tarafından üretilen mükemmel yapılardır ve dört bir yanımızı çevreler. Bir fraktalı tam anlamıyla tanımlamak zor ancak çoğu şu dört ortak özelliği taşır: Sonsuz detay, yakınlaştırma simetrisi, basitlikten gelen karmaşıklık ve kesirli boyutlar. Bir gün bir eğrelti otuna bakmak için biraz duraklayın. Eğrelti otu harika bir fraktal örneğidir. İlk olarak eğrelti otunun şeklinin ne kadar ayrıntılı olduğuna dikkat edin. Yakından incelediğinizde yaprakların, dalların küçük kopyaları olduğunu görebilirsiniz. Dahası, her yaprağın içindeki damarlar da yaprağın ve dalın kopyasıdır.

Fraktallar: Doğanın şaşırtıcı matematiği

Karmaşıklığı sonsuza kadar uzanan bu matematiksel şeklin temelinde tek bir ana şekil vardır ve bu şekil kendini sonsuza dek tekrar ederek bütünü oluşturur. Görüntüyü ne kadar yakınlaştırmış veya uzaklaştırmış olmak fark etmez. Fraktalın her parçası bütüne benzer.

İngilizce fractal kelimesi Latince frāctus kelimesinden geliyor ve "kırılmış" veya "çatlak" manasını taşır. Her fraktalın kesirli bileşenlerden oluştuğu düşünüldüğünde uygun bir ifade.

Bizi hayatın pek çok farklı alanında çevreleyen fraktallar var. Fraktalın özelliğinin ne olduğunu, neden önemli olduğunu ve hayatımızdaki yerini ele alalım. Aşağıda bu bilgilerin yanında fraktala dair sık sorulan sorulara yanıtlar var: Fraktal nedir, nasıl oluşur, ne için kullanılır ve daha fazlası gibi.

Eğrelti otunun tamamı kendini daha küçük boyutlarla tekrar tekrar tekrarlayan aynı temel şekilden oluşur. Hepsinden daha şaşırtıcı olanı fraktal matematiğe göre bu mütevazı eğrelti otu yaprağının ne 1 ne de 2 boyutlu bir şekil olduğunu ancak arada bir yerde yer aldığını gösterir.

İlgili

Merakınızın Arkasındaki Beyin Bölgesini Artık Tam Olarak Biliyoruz

Yağmur Neden Uykuya Neden Oluyor?

Oşinografi'nin İcadı ve Gelişimi

Bu eğrelti otunun tam şekli

Lisede öğretilen klasik Öklid geometrisi bu basit soruyu cevaplayamaz. Silindirler ve dikdörtgenler teknolojinin şekillerini ele alırken işe yarasa da doğal dünyadaki çok az şekil bu kadar normal ve pürüzsüzdür.

Bir eğrelti otunu kesin bir matematiksel şekil olarak nasıl açıklayabilirsiniz? Bu harika nesnenin matematiksel modelini oluşturmak mümkün mü? Tam olarak bunu yapan ve yaklaşık 40 yıl önce literatüre giren fraktal geometri adındaki matematik dalı, doğanın gizemini aydınlatır.

Sonsuz detay

Doğanın pek çok deseni öylesine düzensiz ve parçalıdır ki, Öklid'e kıyasla… doğa sadece daha yüksek bir dereceden değil aynı zamanda tamamen farklı bir tür düzeyden karmaşıklık sergiler.

Benoît Mandelbröt, The Fractal Geometry of Nature

Dünyanın ilk fraktalının keşfi 1861'de yapıldığında matematik camiasında şok dalgaları yarattı. Bir kalem alır ve bir zikzak çizerseniz elinizde düz çizgilerle birbirine bağlanan keskin köşeler olur. Bunu bir seviye yukarı taşıyan Alman matematikçi Karl Weierstrass o kadar sivri uçlu bir zikzak inşa etmişti ki köşelerden başka bir şey değildi.

Pürüzsüz çizgi gibi görünen bir şekil büyütüldüğü anda, hiç bitmeyen köşeler silsilesine dönüşüyordu. Weierstrass'ın şekli mümkün olan her ölçekte daima düzensiz ayrıntılara sahipti–fraktal bir şeklin ilk önemli özelliği bu oldu.

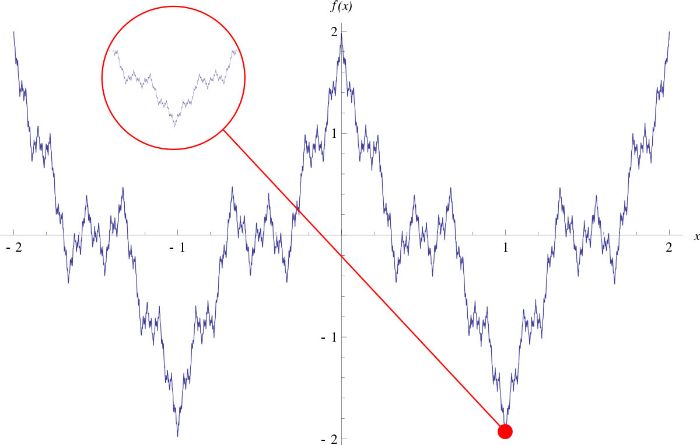
Matematikçiler Weierstrass'ın şekline "patolojik" dediler çünkü bu şekil yüksek titizlikle son birkaç yüz yılda bir araya getirilmiş, doğruluğu denenmiş ve test edilmiş kalkülüs araçlarına meydan okuyordu. Ne var ki bu keşif uzun bir süre matematikçilerin yalnızca yeni bir geometriye attığı kısa bir bakış olarak kaldı… ta ki modern bilgisayarın sunduğu hesaplama gücünün fraktalın kapılarını araladığı 100 yıl sonrasına dek.

Yakınlaştırma simetrisi

Başka bir deyişle, kendimi, geometrisi olmayan şeylerin bir geometrisini oluştururken buldum.

Benoît Mandelbröt, 1924-2010

Fraktal geometrinin yeni bir matematik dalına dönüşmesi büyük ölçüde Polonya doğumlu matematikçi Benoît Mandelbröt ve onun 1977 tarihli ufuk açıcı makalesi The Fractal Geometry of Nature sayesinde olmuştur.

Mandelbröt 1960'larda IBM New York'ta çalıştı. Şirketindeki muazzam bilgi işlem gücü, fraktalın yeni ve tuhaf dünyasını ilk kez keşfetmesini sağladı.

Belki de bugün en çok bilinen fraktal, onun keşfi olan ve adını taşıyan Mandelbröt kümesi olmuştur. Mandelbröt kümesini çizmek imkansızdır. Şekil yalnızca uçtaki her bir noktanın ayrı ayrı özenle boyanmasıyla ortaya çıkarılabilir.

Hangi noktaya hangi rengin uygulanacağını seçmek için basit bir hareket kuralı ele alınır. Hareket noktaya tekrar tekrar uygulanır ve noktanın sayfadan "kaçmasının" ne kadar sürdüğüne bakılır.

Bilgisayar programları fraktallarla ilişkili yeni bir simetri türünün keşfedilmesini sağladı. Matematikçiler için simetri bir aksiyondur ve şekle uygulandığında şeklin (aşağı yukarı) aynı görünmesini sağlar.

Örneğin, bir karenin dönme simetrisine sahip olduğunu söyleriz çünkü bir karenin siz bakmadığınız bir zamanda 90 derece döndürüldüğünü anlamanız mümkün değildir.

Bir fraktaldaki sonsuz karmaşıklık onun, sıradan şekillerde bulunmayan tamamen yeni bir tür simetriye sahip olduğunu gösteriyor. İnanılmazdır ki fraktalın küçük bir bölgesine yakınlaştırmak en başında baktığınız şekli görmenizle sonuçlanır. Fraktalın her bir küçük parçası bütünle tamamen aynıdır.

Buna yakınlaştırma simetrisi deniyor ve sadece matematiksel bir merak değil, doğanın her yerinde bulunabilen bir olgudur—yeter ki aramayı bildiğiniz zaman.

Bir şimşeğe yakınlaştırırsanız ortaya yakınlaştırma simetrisi çıkar—her dal, tüm şeklin küçük bir kopyasıdır.

Basitlikten gelen karmaşıklık

Dipsiz harikalıklar, sonu gelmeyen basit kurallardan gelişir.

Benoît Mandelbröt, 1924-2010

Mandelbröt fraktalları mikroskopla incelerken, İngiliz matematikçi Michael Barnsley (bugün 75 yaşında Avustralya Ulusal Üniversitesi'nde eğitim vermektedir) aynı nesnelere farklı bir açıdan yaklaşmayı düşündü.

Fraktal şekillerin geometrisi sonsuz derecede karmaşık olsa da bir fraktalın üçüncü özelliği karmaşıklığının basitlikten gelişmesidir. Bir fraktalın temel şeklini yakalamak için hangi daha küçük kopyalardan oluştuğuna bakılır. Kopyaların nasıl tekrar ettiği görülür ve küçük bir matematiksel haritalama listesi oluşturulur.

Barnsley'in 1988 tarihli etkileyici kitabı Fractals Everywhere'de Kaos Oyunu adlı bir algoritma vardı. Bu algoritma ile bir bilgisayar herhangi bir fraktal şekli, haritasının bilinen kısımlarına göre hızla oluşturabiliyordu. Kaos Oyunu bir başlangıç ​​noktası alır ve bu nokta etrafında geçiş yaparak hareket ederdi. Her geçiş rastgele bir fraktal haritasının seçilmesiyle yapılıyordu.

Şaşırtıcı bir sonuca varıldı: Başlangıç ​​noktası ve seçilen haritalar ne olursa olsun görüntü hızla "garip çekici" veya strange attractor denilen bir fraktal şekle dönüşüyordu ve şekil sonsuza dek detaylanmaya devam ediyordu. Bugün bu şeklin Kaos Teorisi'nin temelini oluşturduğu düşünülüyor. Sisteme yapılan en ufak bir dürtü noktanın, çekiciden uzaklaşmasını yani kaosu sağlar. Barnsley herhangi bir şekli alıp fraktal haritasını hesaplamanın yolunu bulmuştu. Karmaşık bir şeklin basit haritalarla yeniden oluşturulabileceğini göstermesi, algoritmasının yeni bir resim sıkıştırma alanının doğmasını sağladı. On binlerce resim içeren Microsoft Encarta tek bir CD'ye bu sayede basıldı.

Kesirli boyutlar

Doğa matematikçilere bir şaka yaptı. 19. yüzyıl matematikçileri hayal gücünden yoksun olabilirler ama doğa hiçbir zaman öyle değildi.

Benoît Mandelbröt tarafından The Fractal Nature of Geometry kitabında yer verilen F. J. Dyson sözü.

Tüm fraktalların son ve en çarpıcı özelliği 1, 2 veya 3 boyutlu değil arada bir yerlerde olmalarıdır. Doğanın kesirli boyutlara dair herhangi bir sorunu yok gibi görünüyor, bu yüzden bizim de öyle olmamız gerek. Önce "boyut" ile ne demek istediğimizi açıklamalıyız.

"Boyut" fikrinin birçok farklı (ancak tutarlı) matematiksel tanımı var. Bir şeklin boyutunu, şeklin ne kadar pürüzlü olduğunun bir ölçüsü olarak veya şeklin çevresindeki alanı ne kadar iyi doldurduğunun göstergesi olarak düşünebiliriz.

Düz kağıdı 2 boyutlu olarak düşünebilirsiniz. Çünkü yüksekliği ve genişliği vardır ancak (pratikte) derinliği yoktur. Topu ele alalım. 3 boyutlu dersiniz çünkü ayrıca bir derinliği vardır. Şimdi kesirli boyutu göstermek için, kağıt parçasını alın ve top haline getirin. Ne tam olarak bir top kadar pürüzsüz ne de kağıt kadar düzdür. Kağıt topun yaklaşık 2,5 boyutlu olduğunu söylersiniz.

Benzer şekilde akciğerimiz yaklaşık 2,97 boyutludur. Akciğerimiz birkaç tenis kortu kadar yüzey alanına sahip. Ancak fraktal geometriden oluşuyor olması, geniş yüzey alanının çok daha küçük bir hacme (birkaç tenis topu) sığdırılmasını sağlıyor. Böylesine büyük bir yüzey alanını vücuda yerleştirmek bizi hayatta tutmayı sağlayacak oksijene sahip olmanın tek yolu.

Mütevazı bir eğrelti otundan evrenin en geniş nesnelerine kadar fraktallar çevremizdeki dünyanın her yerindeler. Onlar doğanın arka planında kullanılan üst düzey matematik ve geometridir.

Beynimiz dahil olmak üzere anatomimizin belirli kısımları da fraktaldır. Eğer fraktal şekillere dikkat etmeye başlarsanız bulutlar, bitkiler ve dağlar gibi çok çeşitli nesnelerin fraktaldan oluştuğunu görerek hayran kalırsınız.

Fraktal matematik, sadece doğanın şekillerini modellememize izin vermiyor aynı zamanda çevremizdeki mucizevi dünyaya karşı duyduğumuz hayranlığı yeniden canlandırıyor.

Fraktalın kendine yer bulduğu bazı alanlar şöyle: Doğa, bilgisayarlar, matematik, 3 boyutlu modelleme, bilgi ve veri yönetimi, insan psikolojisi, zaman, ses, sanat, hukuk vb.

Fraktalın önemi

1. Fraktal bir şeklin meydana geliş süreci şaşırtıcı derecede basittir ve klasik geometriden tamamen farklıdır. Klasik geometride bir şekli tanımlamak için formüller kullanılırken fraktal geometri "tekrarı" kullanır. Bu nedenle Pisagor, Platon ve Öklid gibi devlerin çalışmalarından tümüyle farklı bir yöndedir. Klasik geometri 2000 yılı aşkın bir süredir inceleniyor, fraktal geometri ise sadece 40 yıldır göz önünde.
2. Fraktal geometrinin şekilleri doğaya benzer. Bu şaşırtıcı gerçeği görmezden gelmek zordur. Hepimizin bildiği gibi doğa mükemmel daireler ve mükemmel karelerden oluşmaz. Sadece bu da değil, ağaçlara, dağlara veya nehir sistemlerine baktığınızda matematikte kullanılan hiçbir şekle benzemezler. Fraktal geometri, tek bir parçanın yinelenmesinden oluşan ve son derece karmaşık görünen bu doğal durumların arkasındaki formülü anlamamıza ve modellememize izin veriyor. Eğer çevremizdeki doğal şekilleri geleneksel matematiğin basit yaklaşımıyla açıklamayı deneyebiliyorsak, fraktal geometri bunu çok daha kolay, detaylı ve doğru şekilde yapmayı sağlıyor.

Doğadaki fraktallar

Fraktalın temelde ne olduğu anlaşıldığında, doğada kaç tane benzersiz fraktal türü olduğunu görmek çok şaşırtıcıdır. Doğadaki en yaygın fraktal örnekleri arasında ağaç dalları, hayvan dolaşım sistemi, kar tanesi, şimşek, elektrik, bitkiler, yapraklar, coğrafi arazi ve nehir sistemleri, bulutlar, kristaller ve çok daha fazlası var. Tüm bu ortak noktalar kimilerine göre tek bir Tanrı'nın tüm doğada kullandığı ortak matematiğin yansıması olabilir.

Fraktal ağaçlar

Ağaç uzuvlarının büyüme biçimi fraktaldır. Ağacın ana gövdesi fraktalın başlangıç ​​noktasıdır ve ana gövdeden büyüyen her dal dizisi büyümeye devam ettikçe kendi yeni dallarını oluşturur. Büyüme devam eden dallar giderek küçük ve ince bir hal alır. Bir noktadan sonra aynı dallar yeni büyük dallar verebilir ve bu döngü sonsuz bir desen oluşturur. Ağacın her bir dalı bütünün daha küçük ölçekli versiyonu gibidir.

Canlı bedenindeki fraktallar

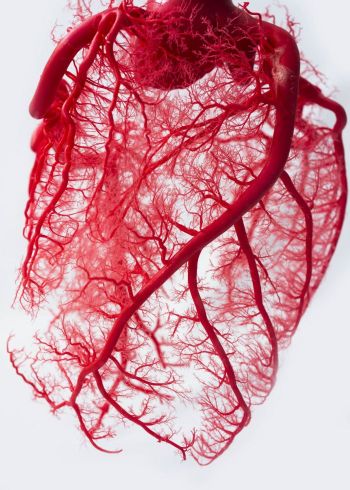
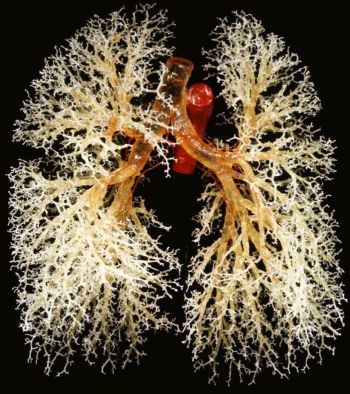
Fraktalların görüldüğü bir başka inanılmaz yer hayvan dolaşım ve solunum sistemi oluyor. Örneğin, insan solunum sistemini ele alırsanız dallanan ve sonunda çok daha ince taneli kollara dönüşen tek gövdeli (ağaca benzer) bir fraktal görürsünüz. Doğanın birçok yerindeki "büyüme" deseni arasında şaşırtıcı bir ortak benzerlik bulunuyor.

Fraktal kar taneleri

Her kar tanesinin benzersiz olduğunu duymuş olabilirsiniz. Kar tanelerinin benzersizliğine katkıda bulunan faktörler arasında inanılmaz miktarda ayrıntı ve çeşitlilik sunan fraktal desenlere sahip olmaları var. Bir buz kristalinde fraktalın başlangıç ​​noktası merkezdedir ve kristal her yöne doğru genişler. Diğer fraktal örneklerinde olduğu gibi şekil kendini her tekrar ettiğinde daha küçük ve daha ayrıntılı hal alır, bu da şeklin genel karmaşıklığını yükseltir.

Fraktal şimşek ve elektrik

Daha önce şimşekli bir fırtına izlediyseniz doğanın en güçlü fraktal gösterilerinden birine ön sıradan yer almışsınız demektir. Elektrik, elektriği iyi iletmeyen (hava gibi) bir ortamdan geçtiğinde oluşan bu model fraktaldır. Bu olayın oluşmasının arkasında elektriğin hava ile kurduğu etkileşim var. Elektrik akımı havadan geçerken havayı aşırı ısındırır. Havanın aşırı ısınması elektrik iletkenliğini değiştirir ve akımın dallanmasını sağlar. Bu süreç her bir dallanmada kendini tekrar eder ve ortaya bir fraktal çıkar. Bir yıldırım çarpması veya elektrik boşalmasının görüntüsünü ters çevirdiğinizde ağaca ne kadar benzediğini göreceksiniz. Bunun nedeni her ikisinin de fraktal olmasıdır.

Bitki ve yapraktaki fraktal

Bir dahaki sefere bir salata, ananas, brokoli veya başka bir yiyecek yediğinizde aslında fraktal yediğinizi hatırlayın. Tıpkı hayvanlarda olduğu gibi bitkiler ve yapraklarda da besinler fraktal ağ aracılığıyla taşınır. İç yapının bu fraktalllığı, sıvıların ve diğer hayati maddelerin bitki içinde dolaşmasını ve her hücreye ulaşmasını kolaylaştırır.

Bazı bitki türleri dışarıdan da fraktal görünür. En dikkat çekici örneklerden biri Romanesco brokolisi adı verilen bir brokoli türü. Bu brokolide tek bir desen var ve bitki büyüdükçe desen kendini tekrar ediyor. En uç noktaya kadar inanılmaz şekilde yinelenmeye devam etmekte (kar tanesi fraktalına benzer).

Eğrelti otu bir başka harika fraktal örneği. Diğerleri gibi eğrelti otları, özünde kendini tekrar eden tek bir şekilden oluşuyor.

Coğrafya, nehir ve arazideki fraktallar

Yıldırım, ağaç ve bitki gibi coğrafya, nehir ve arazi de sıklıkla fraktal özelliği gösterir. Bir arazinin nasıl oluştuğunu ve çöktüğünü ele alırsanız bunun büyük kısmı su erozyonuna bağlıdır. Bir organizmada sıvının dağıtımını sağlayan ağlara benzer şekilde, nehirler ve diğer su kütleleri de suyu fraktal bir yapıyla toplar, taşır ve dağıtır. Bunun en harika örneği bir dereden nehre, göle veya başka bir büyük su kütlesine hareket eden suyun rotasıdır.

Nehir gibi su kütlesi oluşumları coğrafi manzarayı şekillendirir. Su, araziyi fraktallar halinde oyarak yol alır. Kıyı şeridi uzunluğu coğrafyadaki fraktal geometrisi ölçümüne iyi bir örnek. Bir km uzunluğunda bir cetvelle bir kıyı şeridini ölçerseniz, sahil şeridinin ne kadar uzun olduğuna dair çok kaba bir tahmininiz olur. Çünkü tümsek, sırt ve çıkıntı gibi ince ayrıntıları yakalayamazsınız.

Bununla birlikte, cetveli bir metreye kısaltırsanız ölçüm cihazı artık çok daha hassas olduğundan daha ince ayrıntıları yakalamaya başlar. Ölçümün ayrıntı düzeyini her artırdığınızda doğruluğu artar. Kıyı şeridi örneğinde şeridin gerçek çevre uzunluğu artacaktır. Çünkü kıyı şeritleri fraktal geometriye sahipler. Bu ayrıntılar son derece incedir ve çok geniş bir alana yayılır.

Kıyı şeridi geometrisi küpler ile modellenebiliyor. Ancak tüm ayrıntıların elde edilmesi için küplerin çok küçük olması şarttır aksi takdirde detaylar kaybolur. Bunu çözünürlüğe benzetebilirsiniz. Düşük çözünürlüklü görüntüde pikseller büyüktür ve görüntü bulanıktır. Görüntünün çözünürlüğünü artırdıkça pikseller küçülür ve görüntü ayrıntılı hale gelir.

Bulutlardaki fraktal

Bulutlar fraktal özelliği gösterir. Atmosferdeki türbülans, su parçacıklarının birbiriyle etkileşiminde ilginç bir etkiye sahiptir. Bir türbülans doğası gereği fraktaldır ve bu nedenle bulutların oluşumu ve görünümü üzerinde doğrudan etkiye sahiptir. Buluttan yayılan yoğunlaşma, buz kristali ve yağış miktarı bulutun durumunu ve sistemin yapısını, dolayısıyla türbülansı etkiler.

Kristaldeki fraktal

Tıpkı buz oluşumu gibi, mineralden oluşan diğer doğal kristal formları da fraktal özelliğe sahipler. Kristalin türüne ve mineral içeriğine bağlı olarak bazıları diğerlerinden daha fraktal görünür. Bunun iyi bir örneği bazı ametist veya piritin oluşumlarındaki küplü yapıdır.

Doğadaki fraktallara dair daha fazla bilgi için bu fikre öncülük eden Beniot Mandelbrot'un ikonik kitabı The Fractal Geometry of Nature'ı incelemenizi öneririz.

Bilgisayarda fraktallar

Fraktallar dünyamızı çok farklı şekillerde çevreliyor. Ancak fiziksel dünyada görülen fraktalları incelerken ne kadar derine inilebileceğine dair fiziksel sınırlamalar var. Zira çok fazla yakınlaştırırsak molekülleri görmeye başlarız ve fraktal model ortadan kaybolur. Bilgisayarlarda ise hikaye daha farklı. Bilgisayarlar ile fraktalları inanılmaz derecede ayrıntılı düzeyde keşfetme imkanı doğdu ve fraktal, matematiksel denklemden türetildiği için bu şekilleri sonsuz derinlikte keşfetme imkanı elde edildi.

Bir fraktalı araştırmak ve oluşturmak için bilgisayar kullanabilirsiniz. Bilgisayar ayrıca imkansız sayıları hesaplama yeteneğine sahip olduğundan bu durum insanlara birçok farklı gerçek dünya uygulamasında karmaşık fraktal denklemler kullanma yeteneği sunar. Reklam, film, dizi ve video oyunlarındaki 3B modelleme ve arazi modellemede yararlanılan fraktal denklemler projenin gerçekçiliğini artırır.

Bilgi ve veri yönetiminde fraktallar

Örneğin bir web sayfasına baktığınızda bilgiler ayrı ayrı alt kategorilere veya konulara ayrılır. Bu konuların her biri, benzer veya ilgili alt kategorilere azalan oranda bölünebilir. Bilginin fraktalı sonlu olsa da, yapılandırılma biçimi ağacın dallanma modelini andırır. Fraktal teorisini kullanarak bilgi ve içeriğin organizasyonunu ele almaya Hanby İçsel Bilgi Teorisi denildi.

Bilim ve teknolojide fraktal

Fraktalların bilim ve teknolojinin diğer birçok alanında uygulamaları var. Başlıca uygulamalar arasında:

• Fraktal antenler
• Fraktal transistör
• Fraktal ısı eşanjörü
• Dijital görüntüleme ve görüntü sıkıştırma ve dijital fotoğrafı büyütme
• Fraktal sinyal sıkıştırma
• Mimarlık
• Kentsel büyümenin fraktal modellemesi
• Fraktal analiz kullanarak yaşam tespiti
• Zemin mekaniğinde fraktal
• Bilgisayar ve video oyun tasarımı
• Fraktografi ve kırılma mekaniği
• Kaba fraktal sistemlerin küçük açılı saçılma teorisi
• Fraktal kamuflaj desen üretimi, örneğin MARPAT
• Hisse seneti, para birimleri ve diğer emtialar için teknik fiyat analizi.
• İnternet ağlarında fraktallar
• Tıp
• Sismik aktivite çalışması
• Fraktal kullanarak arama ve kurtarma planı oluşturma

Matematikte fraktal

Fraktalın matematiksel inceliklerini araştıran yüzlerce kitap yazıldı. Aşağıda bir fraktalın nasıl matematik formülleriyle temsil edildiği, boyut kavramı ve daha fazlası ele alınıyor.

Fraktal şekiller

Matematik formüllerine derinlemesine girmeden önce, matematik formüllerinden oluşturulan birkaç yaygın fraktala bakalım. Doğadaki fraktallar gibi, matematiksel olanlar da hangi ölçekte bakarsanız bakın özdeştir. Bu durum en kolay düz siyah kare ve üçgenlerde görülür.

Bunlardan birine Sierpinski Üçgeni deniliyor. Tek bir üçgenle başlanır ve ardından her seferinde merkezden bir üçgen çıkartılır. Her tekrarla birlikte üçgen giderek daha boşluklu hale gelir. Ayrıca her yeni üçgen bir sonraki tekrar gibi görünür ve şeklin tamamına çokça benzer.

Fraktal şeklin bir başka harika örneği von Koch kar tanesidir. Sierpinski Üçgeni'ne zıt bir yaklaşımı benimser. Üçgeni çıkarmak yerine üçgen eklenir. Her yinelemede şeklin yan tarafına eklenmiş orantılı bir üçgen bulunur. Sonra bu kenarların her birine başka bir üçgen daha eklenir ve desen sonsuza kadar tekrar eder. Tüm kenarlar arasında öz benzerlik vardır.

Mandelbrot Fraktalı Kümesi'ni oluşturmak

Mandelbrot kümesi zn + 1 = zn² + c formülü izlenerek oluşturuluyor. C, aşağıdaki düzlem ızgarası üzerindeki noktadır. Z, karesi alınmış sayıdır ve C'ye eklendiğinde yeni bir Zn + 1 değerini verir. Seçilen C değeri formülün sonsuz çıkmasına neden oluyorsa seçilen C değeri Mandelbrot kümesinin parçası olamaz. Sayı sonsuza çıkmazsa Mandelbrot kümesine ait demektir.

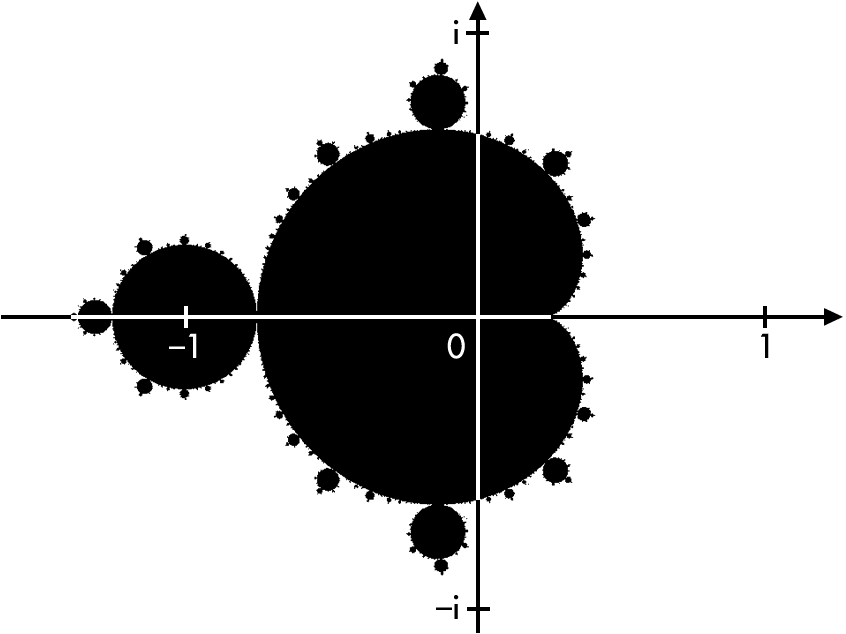
C = 1 Mandelbrot kümesinin parçası olmasın. Bu durumda aşağıdaki formül görülür:

• zn + 1 = zn² + c
• 1 = 0² + 1
• 2 = 1² + 1
• 17 = 4² + 1
• 26 = 5² + 1

Mandelbrot kümesi gibi karmaşık bir şekli oluşturmak için yukarıdaki gibi yüzbinlerce hatta milyonlarca hesaplama yapmak gerekiyor. Formülü kullanarak ne kadar fazla hesaplama yapılırsa fraktalın şekli o kadar ayrıntılı hale gelir. Bilgisayarların son derece hızlı hesaplama yapabilme özelliği insanlara yeni fraktal denklemleri keşfetme imkanı sağladı.

Fraktal Hakkında Sık Sorulanlar

Kaynaklar:

• Mathematics LibreTexts – Fractal
• Frontiers – Fractals